Champ gravitationnel: qu’est-ce que c’est et comment le calculer?
Mais que signifie ce concept ? Comment le calculer ? C’est justement ce que nous allons tenter d’expliquer maintenant!
Qu’est-ce que le champ gravitationnel et qui la découvert?
Harman Smith and Laura Generosa (nee Berwin), graphic artists and contractors to NASA's Jet Propulsion Laboratory, with Pluto removed by User:Frokor, Public domain, via Wikimedia Commons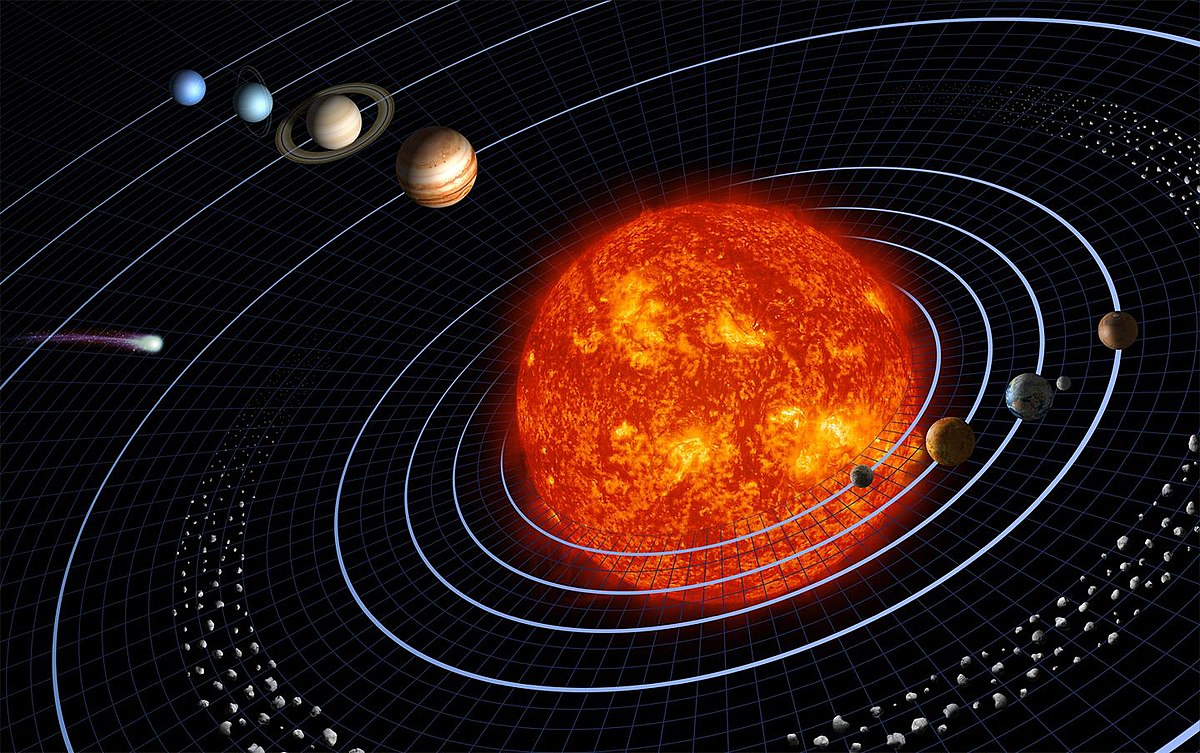
Toute masse, telle que la Terre ou un autre corps céleste, attire à elle tout ce qui l’entoure par la force de gravité. Cette force est décrite, dans le cas le plus simple, par la loi de la gravitation universelle énoncée par Isaac Newton en 1687.
Le champ gravitationnel est une fonction mathématique qui décrit la façon dont une masse modifie l’espace environnant; autrement dit, étant donné une masse et son champ gravitationnel, nous sommes en mesure de calculer la force gravitationnelle qu’elle génère en chaque point de l’espace.
Combien vaut le champ gravitationnel de la Terre?
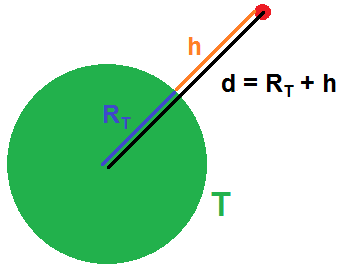
Le champ gravitationnel ainsi expliqué ci-dessus (et calculé) est en fait une version extrêmement simplifiée de la réalité : nous avons en effet supposé que la masse est complètement concentrée en un point, le centre de la Terre.
Et cette hypothèse n’est valable que si la distribution de la masse est parfaitement sphérique, C’est-à-dire si la Terre était une sphère et que sa masse était complètement homogène.
Mais la Terre, comme les autres corps célestes, est en fait aplatie aux pôles et gonflée à l’équateur, elle présente des dépressions et des montagnes et sa composition interne est tout sauf homogène. L’approximation n’est alors valable que si l’on s’éloigne suffisamment de la Terre pour que les irrégularités nous échappent, ce qui rend efficace l’étude du mouvement des planètes par la loi de la gravitation universelle.
Cependant, lorsque nous nous rapprochons, comme dans le cas d’un satellite en orbite terrestre basse, la question se complique et il est nécessaire de prendre en compte les irrégularités afin d’obtenir un calcul plus précis du champ gravitationnel. Cela se fait en ajoutant d’autres éléments aux équations de la gravité dérivées de la loi de la gravitation universelle, connus sous le nom d’harmoniques sphériques, qui créent une approximation progressivement améliorée du champ. La connaissance de ces harmoniques sphériques est cruciale pour le calcul correct des orbites que les satellites doivent suivre.
Mais traduisons maintenant ces propos en chiffres. Considérons, en première approximation, la Terre comme une sphère de 6370 km de rayon. Rappelant la formule du volume de la sphère, nous pouvons en déduire que le volume de la Terre (V) est égal à 1,08 – 1021 m3. Des lois de la physique sur l’attraction gravitationnelle entre les corps dans l’univers, on déduit également la mesure de la masse de la Terre (m), qui est égale à 5,98 – 1024 kg.
À partir de ces deux données, on peut déduire la densité moyenne (d = m/V) de la Terre, qui est de 5,54 g/cm3. Comme les roches qui composent la croûte terrestre, accessibles à l’observation directe, ont une densité moyenne comprise entre 2,7 et 3 g/cm3, on peut en déduire que les matériaux trouvés à plus grande profondeur ont une densité plus élevée, de l’ordre de 10-13 g/cm3.
Les variations locales qui se produisent dans le champ gravitationnel de la Terre (c’est-à-dire la zone d’espace autour d’un corps ayant une masse, dans laquelle d’autres masses sont affectées par son attraction) indiquent que la densité n’est pas uniformément répartie à l’intérieur de la Terre. La valeur moyenne théorique de l’accélération de la pesanteur g est de 9,81 m/sec2.
Comment le champ gravitationnel est représenté sur un plan?
Le champ gravitationnel peut se dessiner sur un plan par des lignes de champ. Celles-ci sont toujours orientées vers la partie centrale du corps et représentent une symétrie radiale. A noter que les lignes de champs deviennent plus fines lorsqu’on s’éloigne du corps plus denses et sont plus denses quand on se trouve proche de la surface.
Quelles sont les différents concepts du champ gravitationnel?
Isaac Newton a été le premier à comprendre que la masse joue un rôle crucial dans l’intensité de la gravité dont le nom vient du latin ”gravis”, qui signifie lourd. Il a également compris que la gravité se manifeste quotidiennement sur Terre par la force du poids et que c’est la même force qui maintient les planètes en orbite autour du Soleil. La loi de la gravitation universelle stipule que deux masses, m1 et m2, s’attirent avec une force, Fg, proportionnelle aux masses elles-mêmes et inversement proportionnelle au carré de leur distance, r, via une constante G.Cela signifie qu’en physique newtonienne classique, plus les masses sont grandes, plus la force d’attraction est grande.
Mais examinons maintenant le champ gravitationnel en physique moderne.
En 1915, Albert Einstein présente la théorie de la relativité générale, dans laquelle il définit la gravité comme une propriété de la matière, et non comme une force. Selon Einstein, une concentration de masse, ou d’énergie, en un point est capable de courber l’espace-temps et d’influencer les particules et masses environnantes. La preuve expérimentale est la lentille gravitationnelle: l’image d’un corps céleste apparaît décalée en raison de la déviation de la lumière lorsqu’elle passe à proximité d’une masse dense.
Pourquoi la force gravitationnelle existe et comment est-elle créée?
Pourquoi la force gravitationnelle existe-t-elle ? Personne ne le sait. On sait qu’en mettant plus d’atomes ensemble, plus de particules ayant une masse, le champ gravitationnel augmente précisément parce que la masse augmente. Mais pour un atome, la gravité est si faible qu’elle n’affecte pas du tout sa structure. Pour ressentir la gravité, il faut avoir beaucoup de masse, donc les étoiles, les planètes, les galaxies, mais aussi les petites masses comme les particules élémentaires ressentent et produisent la gravité, sauf que les valeurs de la force sont si faibles qu’elles ne l’affectent pas.
Certaines théories des champs gravitationnels attribuent la gravité à une distorsion de l’espace-temps produite par une énergie localisée, ou décrivent la gravité au niveau microscopique par l’échange de particules médiatrices de force appelées gravitons.
Plus les gravitons sont échangés, plus la force est intense, donc plus l’énergie est localisée, plus les gravitons sont échangés et plus la gravité est grande. Mais si vous voulez savoir ce que fait cette force étrange au niveau atomique, la réponse est simple : même si elle n’était pas là, rien ne changerait.
Au niveau planétaire et cosmique, cependant, c’est la gravité qui structure le monde que nous connaissons…
Quelle est la formule du champ gravitationnel?
Selon la loi de la gravitation universelle, si l’on désigne par m1 la masse d’un corps, par m2 la masse de l’autre et par r la distance de leurs barycentres, on obtient la formule de base de l’accélération de la pesanteur suivante: F = G (m1 m2) / r2.
F étant la force qu’un corps exerce sur l’autre, et G étant la constante gravitationnelle de la terre (dans ce cas), nous concluons que G = 6,673 10-11 N m2/kg2. Elle sert à définir la force exercée entre deux corps en raison de leur attraction mutuelle.
Il faut ajouter que chaque corps développe son propre champ gravitationnel (H). Nous en déduisons que : H = – G m / r2. Dans ce cas, r indique la distance du centre de gravité de ce corps par rapport au point de l’espace considéré. Attention, ici, au signe d’accélération de la gravité. Le moins négatif que vous voyez dans la formule signifie que la direction de H est vers le centre du corps.
L’intensité de ce champ sur Terre, par contre, est représentée par la formule: H0 =-GM/r02 =9,81m/s2. Où M = la masse de la planète et r0 = le rayon moyen de la planète.
