Die Fibonacci-Folge unter uns

Wir fügen Zahlen hinzu, um die Frage zu beantworten, welche oder wie viele. Was bedeutet zum Beispiel 2 + 2 =? Wenn Sally 4 Äpfel hat und Jane 3 Äpfel, wie viele Äpfel haben sie zusammen? Was passiert jedoch, wenn jede Folgezahl die Summe der beiden Zahlen ist, die vor ihr stehen? Das ist die Fibonacci-Folge. Was macht diese mathematische Formel so besonders?

Der Geheimcode der Natur

Es klingt nach einer Verschwörungstheorie. Zugegebenermaßen neigen Menschen dazu, nach Mustern in Dingen zu suchen, die vielleicht ein Muster haben, vielleicht aber auch nicht. Was wir wissen ist, dass einige Muster der Fibonacci-Folge folgen. Jedoch gilt das nicht für die gesamte Natur.

Die Fibonacci-Folge beginnt so: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 und immer so weiter. Jede Zahl ist die Summe der beiden vorherigen Zahlen. Aber erstreckt sich dieses System zur Nummerierung in den Kosmos?

Beispiele für die Fibonacci-Folge:

• Ein spiralförmiges Muster in Samen entspricht oft der Reihenfolge. Zum Beispiel zeigt der Kopf einer Sonnenblume ein Spiralmuster auf.
• Kiefernzapfen weisen sich abwechselnde Spiralen auf. Jeder Zapfen besteht aus einem Spiralenpaar, die sich jeweils in entgegengesetzte Richtungen nach oben drehen.
• Schneckenhäuser zeigen die Sequenz zusammen mit der Theorie des Goldenen Rechtecks. Im Goldenen Rechteck ist das Verhältnis der Seiten a/b gleich dem Goldenen Mittelwert (phi). Dies führt zu einem Schachtelungsprozess in die Unendlichkeit und nimmt die Form einer Spirale an. Andere Beispiele dieser Spirale kommen bei einigen Ziegenhörnern und Spinnennetzen vor.
• Wirbelstürme drehen sich spiralförming aus dem Auge des Sturms heraus.

Die Geschichte von Fibonacci

Wann hat der Mensch diese Folge entdeckt? Einige Untersuchungen deuten darauf hin, dass die Fibonacci-Folge von Leonardo Fibonacci stammt. Er wurde um 1170 geboren und war ursprünglich als Leonardo von Pisa bekannt. Laut einem Buch von Keith Devlin von der Stanford University sind diese Informationen falsch.

„Leonardo von Pisa hat die Folge nicht wirklich entdeckt,“ sagte Devlin, der auch der Autor ist von “Finding Fibonacci: The Quest to Rediscover the Forgotten Mathematical Genius Who Changed the World,” (Princeton University Press, 2017, Deutsch: “Die Suche nach Fibonacci, dem vergessenen mathematischen Genie, das die Welt verändert hat“). Uralte Sanskrit-Texte, die das Hindu-arabische Zahlensystem anwendeten, erwähnen erstsmals Hunderte von Jahren vor Leonardo von Pisa. ”(Devlim, 2017)

Devlin führt weiter aus, dass die Folge seit dem Beginn der Zeit existiert.

Eine Erklärung der Mathematik

Nachfolgend findest du eine Erklärung der Mathematik hinter der Folge.

Die Fibonacci-Sequenz arbeitet mit dem Goldenen Schnitt. Das Verhältnis der Zahlen in der Folge, während die Folge ins Unendliche weitergeht, nähert sich dem Goldenen Schnitt.

Der Goldene Schnitt ist eine spezielle Zahl, die durch Teilen einer Linie in zwei Teile ermittelt wird, so dass der längere Teil geteilt durch den kleineren Teil ebenfalls der gesamten Länge geteilt durch den längeren Teil entspricht. Es wird oft nach dem 21. Buchstaben des griechischen Alphabets mit phi symbolisiert. In einer Gleichung sieht es so aus:

a/b = (a+b)/a = 1.6180339887498948420 (Live Science, 2018)

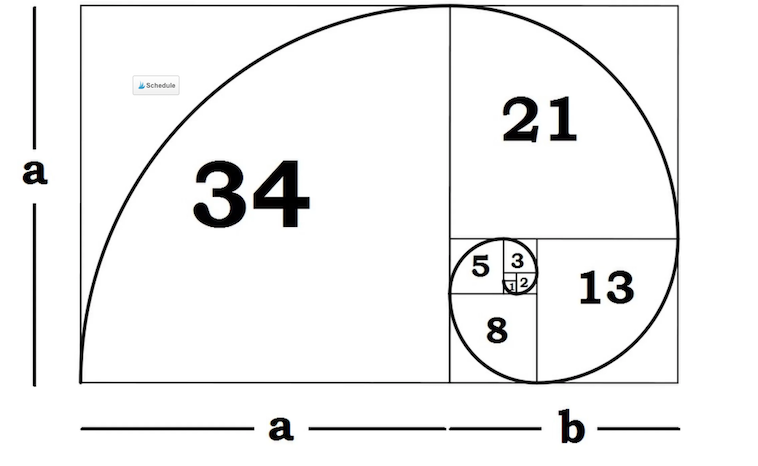
Von dort aus können Mathematiker berechnen, was als goldene Spirale oder logarithmische Spirale bezeichnet wird. Sein Wachstumsfaktor entspricht dem Goldenen Schnitt.

Erkennst du Muster, die zur Definition der Fibonacci-Folge passen? Viele meinen, dass Spiralgalaxien passen, aber wir können sie ehrlich gesagt nicht messen. Auf jeden Fall sorgt es für eine gute Unterhaltung während des Abendessens und gibt uns mehr zu bedenken, hinsichtlich der Entstehung aller Dinge in der Natur.