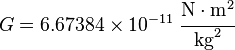Newton y la ley de la gravitación universal

Fue el físico inglés Isaac Newton quien primero enunció la ley de la fuerza de gravitación en el siglo XVII. Años más tarde. él mismo desarrollará lo que hoy en día se conoce como cálculo integral, y que está estrechamente relacionado con la gravitación. Dicha fuerza afecta a todos los cuerpos por tener esos una masa propia, y permite que los dos, o más se atraigan entre sí.
El matemático inglés, Newton, nació en la región del Lincolnshire en el diciembre del 1642. Ya a los tres años, cuando su madre enviudó, fue criado por su abuela. Luego sus estudios primarios, en el verano de 1661, llegó a ser profesor tras ingresar en la Universidad de Cambridge.
¿Cómo llegó Newton a la ley de gravitación universal? Todo el mundo conoce la leyenda según la cual el estudioso inglés estaba sentado debajo de un manzano reflejano sobre el motivo y la fuerza que mantiene unida la Luna y la Tierra, cuando vio caer una manzana del arbol. Este hecho le hizo pensar que la fuerza que atrae al suelo la manzana es la misma fuerza que padece la Luna y eso le permitió teorizar la ley de la gravitación universal. Sin embargo, la ley fue el resultado de una larga investigación matemática de Newton en el siglo XVII.
Fueron años de estudio intenso, durante los cuales Newton profundizó asuntos sobre algunas asignaturas científicas, entre ellas, matemáticas y astronomia. Algunas de sus investigaciones le llevaron a notables descubrimientos en la rama de la física y por consecuencia en el asunto de la gravitación universal.
Durante esa época, el físico inglés pudo formular la ley de la gravitación universal, presentada en su libro «Philosophiae Naturalis Principia Mathematica», publicado en 1687. Según esta ley, basada empíricamente en la observación directa de los objetos, la fuerza con que se atraen dos cuerpos de masa distinta depende sólo del valor de sus masas y del cuadrado de la distancia que los separa. Esta ley implica la presencia de una constante, llamada G, cuyo valor no pudo ser establecido de Newton. Esta constante representa la fuerza de atracción entre los cuerpos que actualmente, después de ser repetida y estudiada por otros experimentadores, presenta el siguiente valor aproximado:
Si se quiere conocer el campo gravitatorio de un cuerpo con masa propia, hay que tener presente y establecer la aceleración de ese cuerpo en la órbita de dicho campo. Al aplicar los valores de la gravedad y de una masa conocida mediante la segunda ley de Newton, se puede calcular la aceleración de la gravedad.
La aceleración de los cuerpos celestes
Dicha aceleración es diferente en cada cuerpo, dependiendo del tamaño de este último, es decir, de su masa. Por ejemplo, es evidente que la masa de la Tierra presenta una aceleración mayor a la de la Luna (9,8 m/s² vs. 1,6 m/s²). Por lo contrario, un planeta más grande que la Tierra, tendrá una aceleración mayor con respecto a ésta. La de Júpiter es por ejemplo de 24,9 m/s².
Si tomamos como ejemplo dos cuerpos, uno de los cuales con masa menor respecto al del centro, y el de masa menor que orbita alrededor del de masa mayor, podemos observar que en este caso la fuerza centrífuga y la fuerza centrípeta presentan el mismo valor. En este caso la gravitación universal permite que los dos cuerpos no choquen y que las dos fuerzas se anulen entre sí.
Esta consideración nos permite de recuperar y explicar la tercera ley de Kepler, que resume el hecho de que los planetas que se encuentran más alejados del Sol, tardan más tiempo en dar una vuelta alrededor de este. Gracias a estas leyes ha sido posible conocer y profundizar el conocimiento del sistema solar, y el movimiento de los satélites como la Luna. A pesar de ser tan viejos, estos principios siguen siendo considerados importantes y vigentes para la mayoría de los calculos que atañen a la gravedad.
La ley de gravitación universal explica bastante bien el movimiento de un planeta alrededor del Sol o de un objeto como un satélite bastante cercano a la Tierra. Aunque, en el siglo XIX no se lograban explicar algunos fenómenos, como el de la órbita de Mercurio que no parece formar una elipse cerrada según la teoría de Newton, sino una elipse que sigue rotando en cada órbita, de tal manera que el punto más cercano al Sol se desplaza poco a poco cada siglo en un movimiento que se define como precesión. Por este motivo, se pensó en la existencia de otro planeta más cercano al Sol al que se llamó Vulcano y que no se podía ver por motivo del brillo solar. Sin embargo, el planeta se descubrió que en realidad no existía y sólo con el descubrimiento de la Relatividad de Einstein el problema pudo resolverse.
De todas formas, existen actualmente algunos problemas de observación que no se pueden explicar con la ley de Newton: como hemos visto poco antes, la órbita de Mercurio es una especie de eclipse no cerrada que varía su perihelio cada siglo. Por este motivo, la ley de Newton se puede aplicar a cuerpos de poca masa o de grandes distancias y a la mayoría de los planetas del Sistema Solar excepto Mercurio ya que se encuentra muy cercano al Sol.
Otro asunto es el problema de la velocidad de rotación de las galaxias que no responde correctamente a la ley de la gravitación universal, lo cual ha creado la teoría de la materia oscura o de una dínamica newtoniana modificada. La tercera ley de Kepler afirma que el periodo de rotación aumenta con la distancia a la que se encuentra de otro cuerpo masivo. Si esta ley la aplicamos a las estrellas de una galaxia, lo mismo debería acaecer a los astros más alejados del centro de la galaxia, pero esto es algo que puede ser explicado si en dicha galaxia existiera más masa de la que puede notarse, la cual se llamaría materia oscura, puesto que es materia que no vemos.